marspaar is a creative technologist who worked on large scale platforms as well as various art projects and photography. He also ran a magazine for 10 years that was nominated for the BRIC Award in London.
MetaHarmon
His current work is characterized by the introduction of a mediation scheme between creator and work, consisting of program and programming language, with which a division of labor is linked through the man-machine interface in the aesthetic process.
With a limit of 150 unique NFT collectibles, MetaHarmon presents the first scarce digital art that introduces the harmonograph to the blockchain. MetaHarmons are rare, but some are rarer than others. For example, H 69 is present only once due to its unique shape. Each MetaHarmon has a dimension of of 6000px x 6000px @ 150dpi.
Genesis and development
In the artwork, there is a relation of part and whole that can be symbolically interpreted in terms of human life. The convergence of virtually augmented physical reality and physically persistent virtual space creates a collective virtual space. marspaar is fascinated by the emerging decentralized economy, through which a multitude of new digital-native assets, spaces, and experiences are created. Old and new worlds merge into each other. Because of this he used a Python script to create an allegorical transformation between the harmonograph as an archaic scientific device from the physical world and the metaverse, in which the oscillations of the pendulums propagate into the virtual world.
The Harmonograph
Harmonographs are simple yet fascinating archaic scientific devices that can reveal to us some of the complex, mysterious and beautiful patterns that lie hidden in simple harmonic motion, such as pendulums and rotating wheels.
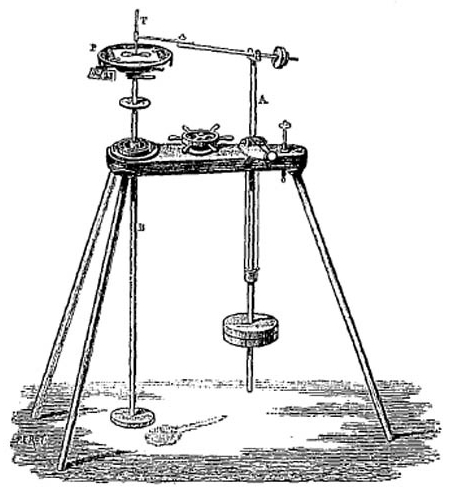
The harmongraph was pioneered in 1844 by Hugh Blackburn, a professor of mathematics at the University of Glasgow. The first harmonograph by the French physicist Jules Antoine Lissajous in 1857 actually used a light beam on a screen instead of the pens on paper that are used today.

Following the invention of the harmonograph, it became a popular device, which was found in many homes. After the early 1900s it decreased in popularity and is rarely seen today.
However, they have been rediscovered in art for some time now. Olafur Eliasson exhibited his installation of a harmonograph in Vienna in 2006. The occasion was the awarding of the Kiesler Prize for Architecture and Art to Eliasson.
Computer-generated Harmonograph
A harmonograph creates its figures using the movements of damped pendulums. The motion resulting as a combination of perpendicular oscillations depends on the ratio of angular frequencies, ratio of amplitudes and phase of contributing oscillations. If the angular frequency ratio is a rational number, the resulting curves are periodic. The curves become non-periodic and very complex if this ratio is an irrational number. If the ratio of angular frequencies is within an approximately ± 10% tolerance from a rational number, the curves become more regular. The shape of the curves is very sensitive to the angular frequency ratio. Damping also increases the complexity of the curves.
The shapes thus generated are stills of a kinetic sequence produced by harmonically-related sinusoidal waveforms. They are essentially an elaboration of the Lissajous figure oscillographic technique used by engineers for frequency measurement. The very large number of different graphic forms are archived by varying the ratio of the frequencies of the waveforms.
The movement of damped pendulums can be modeled mathematically by trigonometric functions and is described by equations. The Python script used by marspaar translates those equations into a graph that emulates a harmonograph. Applying the first equation a second time to each equation can emulate a moving piece of paper.
Want to say hi? Feel free to get in touch via Twitter or